Note: This post was originally published by Luis Natera on his personal blog. It has been republished here as part of TYN Studio's content.
Today marks the birthday of Leonhard Euler, born April 15, 1707. Euler was a Swiss mathematician who made important and influential discoveries in many branches of mathematics, but for those of us working in network science, he's particularly important as the founder of graph theory.

The Seven Bridges of Königsberg
Euler's connection to graph theory stems from his 1735 solution to the Seven Bridges of Königsberg puzzle. The city's seven bridges across the Pregel River prompted the question: "Can one walk across all seven bridges and never cross the same one twice?"
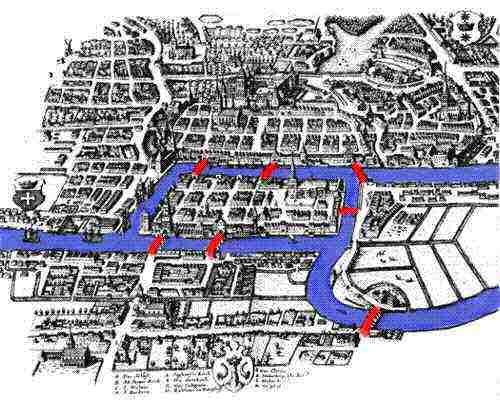
At first glance, this seems like a simple routing problem. But Euler's genius was in how he approached it—not by trying different paths, but by abstracting the problem to its essential structure.
The Abstract Representation
Euler's breakthrough involved representing land areas as labeled nodes (A, B, C, D) and bridges as connecting lines—creating what we now recognize as a graph. This abstraction stripped away all the unnecessary details (the size of the landmasses, the length of the bridges, the width of the river) and focused on pure connectivity.
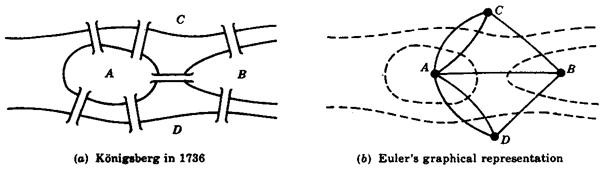
His key insight was identifying that nodes with odd-numbered connections must serve as path endpoints. Think about it: every time you enter a node (except the start), you must also leave it—consuming two edges. So any node you pass through needs an even number of edges.
Since all four nodes in Königsberg had odd degrees (each landmass connected to an odd number of bridges), no valid solution existed. You can't traverse all bridges exactly once because you'd need exactly zero or two odd-degree nodes, not four.
Modern Applications
Today, network science applies Euler's abstraction to study:
- Epidemics: How diseases spread through contact networks
- Urban mobility: How people move through transportation systems
- Social systems: How information flows through relationships
- Economic systems: How money and goods move through markets
- Biological networks: How proteins interact in cells
Multiplex Networks in Urban Planning
The article specifically highlights using multiplex networks—where transportation infrastructure layers (pedestrian, bike, subway, street) map to individual network layers—to analyze city connectivity and identify underserved areas.
This is a direct extension of Euler's thinking: represent the system as a network, analyze its structure, and use that analysis to understand the system's behavior and limitations.
The Power of Abstraction
Euler's lasting contribution wasn't just solving a puzzle about bridges. It was showing that by representing systems as networks of nodes and edges, we can reason about their properties in general terms. The same mathematical insights apply whether we're talking about bridges, roads, neural connections, or social relationships.
That's the power of abstraction—and it all started with a Swiss mathematician wondering about bridges in Königsberg nearly 300 years ago.